2. NumPy 快速上手：数组与向量化计算

本章，你将学到：

ndarray 核心概念：理解 NumPy 数组的 shape, dtype, 和 axis。
数组的创建: 掌握从列表、函数及特殊矩阵创建数组的方法。
索引与切片: 从基础索引到高级的布尔索引和花式索引。
核心操作: 学习广播、形状变换（reshape, .T, newaxis）、拼接、排序和矩阵乘法。
常用计算: 掌握向量化运算（ufuncs）、描述性统计、条件化赋值 (np.where) 和集合操作。

温馨提示

配套资源：本章所有代码和配套资源可以点击如下连接下载——练习 Notebook、示例数组 my_array.npy 与示例数组集合 my_arrays.npz。下载后，可在本地 Anaconda 环境（如 JupyterLab / Jupyter Notebook）中打开并运行这些文件以复现示例和练习。

NumPy: Python 数据科学的基石

NumPy (Numerical Python) 是 Python 中用于科学计算的核心库。它不仅是 Pandas、Matplotlib、Scikit-learn 等几乎所有数据科学库的底层依赖，其本身也极为强大。

为什么它如此重要？

性能: NumPy 的核心是 ndarray (N-dimensional array) 对象，它在底层是使用 C 语言实现的。这使得对数组的操作（向量化计算）可以摆脱 Python 解释器的性能瓶颈，速度远超原生的 Python 列表循环。
功能: 它提供了大量用于数组操作的函数，涵盖了从线性代数到傅里叶变换再到复杂的随机数生成的各种功能。
简洁: NumPy 允许你用非常少的代码来表达复杂的数据操作，让代码更易读、更易维护。

本章将带你掌握 NumPy 最常用、最重要的核心功能。强烈建议你边读边在 Jupyter Notebook 中亲自敲一遍代码。

有用链接:

NumPy 官方网站

NumPy 官方入门教程

准备工作

在开始之前，我们需要导入 NumPy 库。业界惯例是将其重命名为 np。同时，为了让我们的随机数示例可以复现，我们创建一个现代的随机数生成器实例。

import numpy as np

# 使用现代的、推荐的随机数生成器，并设置种子以保证结果可复现
rng = np.random.default_rng(seed=42)

提示

本章及后续章节会介绍许多用于数据处理的函数，这些函数通常包含多种参数。为便于理解，我们在参数说明中使用“(必选)”与“(可选)”来标注：标注为(必选)的参数在调用时必须提供；标注为(可选)的参数可根据需要省略，函数将使用其默认值。举例来说，np.array(object, dtype=None) 中的 dtype 是可选的，既可以写成 a = np.array([1, 2, 3], dtype=np.float64)，也可以简化为 a = np.array([1, 2, 3])，此时 dtype 会采用默认的 None。

一、创建 `ndarray`：构建你的数据块

我们处理数据的第一步，通常是创建 NumPy 的核心数据结构——ndarray。这一步的重点是学会如何将已有的 Python 列表等数据转化为数组，或者根据需要生成特定结构（如全零矩阵）和序列的数组，为后续的计算分析准备好“原材料”。

1. 从 Python 列表创建

这是最基本、最常见的数组创建方式。你可以使用 np.array() 函数，将一个 Python 列表（或嵌套列表）直接转换成一个 NumPy 数组。在转换时，你还可以通过 dtype 参数明确指定数组中元素的数据类型，比如 np.float64 或 np.int32，这对于保证计算精度和内存效率很重要。

np.array(object, dtype=None)

参数	说明
`object`	（必选）任何可迭代对象（如列表、元组或嵌套结构），作为数组的数据来源。
`dtype`	（可选）明确指定目标数组的元素类型，未提供时由 NumPy 自动推断。

# 将一个嵌套列表转换为一个二维浮点数数组
list_data = [[1, 2, 3], [4, 5, 6]]
a = np.array(list_data, dtype=np.float64)

print("从列表创建的数组:")
print(a)

2. 使用内置函数创建占位符数组

在很多情况下，我们需要一个特定形状的数组，但其内容稍后才会通过计算填充。NumPy 提供了一系列函数来快速创建这类“占位符”数组。

np.zeros(): 创建一个所有元素都为 0 的数组。这在初始化权重或累加器时非常有用。

np.zeros(shape, dtype=float)

参数	说明
`shape`	（必选）指定输出数组的形状，可以是整数或元组，例如 `(2, 3)`。
`dtype`	（可选）设置数组元素的数据类型，如 `np.float32`。

# 创建一个 2x3，所有元素为 0 的数组，并显式指定元素类型
zeros_arr = np.zeros((2, 3), dtype=np.float32)

print("\n全零数组:")
print(zeros_arr)
print(f"dtype: {zeros_arr.dtype}")

np.ones(): 创建一个所有元素都为 1 的数组。常用于创建基准矩阵或掩码。

np.ones(shape, dtype=float)

参数	说明
`shape`	（必选）指定输出数组的形状。
`dtype`	（可选）控制数组元素类型，默认与 `np.zeros` 相同。

# 创建一个 2x3，所有元素为 1 的数组，并设置为整数类型
ones_arr = np.ones((2, 3), dtype=np.int64)

print("\n全一数组:")
print(ones_arr)
print(f"dtype: {ones_arr.dtype}")

np.full(): 创建一个所有元素都为指定常数值的数组。当你需要一个特定大小、填充了非零非一常数的数组时使用。

np.full(shape, fill_value, dtype=None)

参数	说明
`shape`	（必选）输出数组的形状。
`fill_value`	（必选）填充值，可以是标量或可广播的数组。
`dtype`	（可选）指定数组元素类型。

# 创建一个 2x3，所有元素为 7 的数组
full_arr = np.full((2, 3), 7, dtype=np.int32)

print("\n指定值数组:")
print(full_arr)
print(f"dtype: {full_arr.dtype}")

np.eye(): 创建一个单位矩阵（Identity Matrix）。单位矩阵是一个方阵，其主对角线上的元素为 1，其余元素为 0。它在线性代数中扮演着重要角色。

np.eye(N, M=None, dtype=float)

参数	说明
`N`	（必选）方阵的行数。
`M`	（可选）列数；未提供时等于 `N`。
`dtype`	（可选）指定矩阵元素类型。

# 创建一个 3x3 的单位矩阵，并强制使用浮点数类型
eye_mat = np.eye(3, dtype=np.float64)

print("\n单位矩阵:")
print(eye_mat)
print(f"dtype: {eye_mat.dtype}")

3. 创建序列数组

生成有规律的数值序列是另一个常见需求，例如用于生成图表的坐标轴或进行序列分析。

np.arange(): 类似于 Python 内置的 range() 函数，但它返回的是一个 NumPy 数组。你可以指定起始值、终止值（不包含）和步长。

np.arange(start, stop=None, step=1)

参数	说明
`start`	（可选）序列的起始值；仅提供一个参数时，该值会被视为 `stop`，起始默认 0。
`stop`	（必选）序列的终点（不包含），仅在提供 `start` 时必填。
`step`	（可选）步长，可以为整数或浮点数。

# 生成一个从 0 开始，步长为 2 的序列
arange_arr = np.arange(0, 10, 2)

# 使用浮点步长生成序列
arange_float = np.arange(0, 1, 0.2)

print("\n使用 arange 创建的序列:")
print(arange_arr)

print("\n使用浮点步长创建的序列:")
print(arange_float)

np.linspace(): 在一个指定的闭区间内，生成指定数量的等间距点。这在需要精确控制样本点数量时非常有用。

np.linspace(start, stop, num=50, endpoint=True)

参数	说明
`start`	（必选）序列起点。
`stop`	（必选）序列终点。
`num`	（可选）采样点数量。
`endpoint`	（可选）是否包含终点，默认 `True`。

# 在 [0, 1] 闭区间内，均匀生成 5 个点
linspace_arr = np.linspace(0, 1, 5)

# 排除终点生成同样数量的点
linspace_open = np.linspace(0, 1, 5, endpoint=False)

print("\n使用 linspace 创建的序列:")
print(linspace_arr)

print("\n排除终点的 linspace 序列:")
print(linspace_open)

4. 创建随机数组

随机数在模拟、抽样、数据增强和初始化机器学习模型参数时至关重要。我们推荐使用现代的 np.random.default_rng() 生成器，它提供了更丰富、性能更好的随机数生成方法。

rng.random(): 在 [0.0, 1.0) 区间内生成服从均匀分布的随机浮点数。

rng.random(size=None)

参数	说明
`size`	（可选）指定输出数组的形状，省略时返回单个浮点数。

# 创建一个 2x3 的数组，其元素在 [0, 1) 区间内均匀分布
rand_arr = rng.random((2, 3))

print("\n均匀分布随机数组:")
print(rand_arr)

rng.standard_normal(): 生成服从标准正态分布（均值为 0，方差为 1）的随机浮点数。

rng.standard_normal(size=None)

参数说明

size （可选）指定输出数组的形状。

参数	说明
`size`	（可选）指定输出数组的形状。

# 创建一个 2x3 的数组，其元素服从标准正态分布
randn_arr = rng.standard_normal((2, 3))

print("\n标准正态分布随机数组:")
print(randn_arr)

rng.integers(): 在指定的整数范围内生成随机整数。

rng.integers(low, high=None, size=None, dtype=np.int64)

参数	说明
`low`	（必选）最小可能值（包含）。
`high`	（可选）最大可能值（不包含）；缺省时区间为 `[0, low)`。
`size`	（可选）指定输出数组形状。
`dtype`	（可选）设置输出整数类型。

# 创建一个 2x3 的数组，其元素为 [0, 10) 范围内的随机整数
randint_arr = rng.integers(0, 10, size=(2, 3), dtype=np.int32)

print("\n随机整数数组:")
print(randint_arr)
print(f"dtype: {randint_arr.dtype}")

5. 数组的基本属性

每个 NumPy 数组都自带一些描述其自身的属性，无需计算即可直接访问。

shape: 数组的维度。例如 (2, 3) 表示 2 行 3 列。
dtype: 数组元素的数据类型，如 int64, float64。
ndim: 数组的轴（维度）的数量。
size: 数组元素的总数。

# 获取并打印数组 a 的属性
arr_shape = a.shape
arr_dtype = a.dtype
arr_ndim = a.ndim
arr_size = a.size

print(f"\n数组 a 的属性:")
print(f"Shape: {arr_shape}, DType: {arr_dtype}, NDim: {arr_ndim}, Size: {arr_size}")

二、索引与切片：精准获取数据

一旦数组创建好，我们就需要从中提取有用的数据子集。这就像在地图上找到特定的坐标或区域，是数据筛选和预处理的关键技能。

有用链接:

NumPy 索引官方文档

# 首先，创建一个 4x5 的随机整数矩阵用于演示
M = rng.integers(10, 100, size=(4, 5))
print(f"Original Matrix M:\n{M}")

1. 基础索引与切片

基础索引和切片是最直接的数据获取方式，可以帮助我们拿到单个元素、一整行、一整列，或者一个矩形的子区域。

获取单个元素: 使用 [row, col] 的语法。

# 获取第1行，第2列的元素 (索引从0开始)
element = M[0, 1]
print(f"\nElement at (0, 1): {element}")

切片获取子数组: 使用 [start:stop:step] 语法，可以对每个维度进行切片。

# 获取第2行到第3行，第3列到第4列的区域
sub_array = M[1:3, 2:4] 
print(f"\nSub-array (a view):\n{sub_array}")

视图 (View) vs. 拷贝 (Copy): 为了性能，NumPy 的基础切片默认返回视图，它与原数组共享内存。这意味着修改视图会直接影响原数组。这是一个非常重要的特性，但也容易出错。

# 修改子数组视图的第一个元素
sub_array[0, 0] = 999 
print(f"\nOriginal M after modifying view:\n{M}") # 原数组 M 也被改变了！

# 如果你需要一个完全独立的副本，而不是视图，必须显式使用 .copy() 方法。
sub_copy = M[1:3, 2:4].copy()
sub_copy[0, 0] = 111 # 修改副本
print(f"\nOriginal M after modifying copy:\n{M}") # 原数组 M 未受影响

2. 布尔索引

布尔索引让我们能根据一个或多个条件来筛选数组中的元素，例如，选出所有及格的分数，或所有销售额大于特定值的记录。这是非常强大的数据筛选方法。

单一条件: 创建一个与原数组形状相同的布尔数组（True/False），然后用它来选择元素。

# 1. 创建布尔掩码：M 中所有大于 50 的元素位置为 True
bool_mask = M > 50
print(f"\nBoolean Mask (M > 50):\n{bool_mask}")

# 2. 使用掩码进行索引，返回一个一维数组，包含所有满足条件的元素
elements_gt_50 = M[bool_mask]
print(f"\nElements > 50: {elements_gt_50}")

复合条件: 使用 & (与) 和 | (或) 操作符组合多个条件。注意：必须使用 & 和 |，而不是 Python 的 and 和 or，并且每个条件都必须用括号 () 括起来。

# 选出 30 到 70 之间的数据
combined_mask = (M > 30) & (M < 70)
elements_between_30_and_70 = M[combined_mask]

print(f"\nElements between 30 and 70: {elements_between_30_and_70}")

3. 花式索引 (Fancy Indexing)

当我们想按照一个不规则的顺序或者一个特定的列表来选取数组的行或列时，就需要用到花式索引。它使用一个整数数组或列表来指定索引。

选取特定的行或列:

# 按照 0, 3, 1 的顺序获取行
fancy_rows = M[[0, 3, 1]]
print(f"\nRows 0, 3, 1 in that order:\n{fancy_rows}")

选取特定坐标的元素: 传入两个索引数组，第一个是行索引，第二个是列索引。

# 获取 (0,1), (1,3), (2,0) 这三个特定位置的元素
specific_elements = M[[0, 1, 2], [1, 3, 0]]
print(f"\nSpecific elements at (0,1), (1,3), (2,0): {specific_elements}")

三、核心数组操作

1. 形状变换

我们拿到的数据在维度上不一定符合分析要求。例如，可能需要将一维长向量转换为二维矩阵才能进行后续的线性代数运算。形状变换就是用来调整数组维度结构的工具。

reshape(): 在不改变数据的情况下，赋予数组一个新的形状。

array.reshape(newshape)

参数	说明
`newshape`	（必选）目标形状，可以是整数或元组，且元素总数需保持不变。

data = np.arange(12)
print(f"Original 1D data: {data}")

# 将一维数组变为 3x4 的二维数组
reshaped = data.reshape(3, 4)
print(f"\nReshaped to 3x4:\n{reshaped}")

ravel() vs flatten(): 将多维数组展平为一维。

.ravel() 速度更快，因为它尽可能返回一个视图（View），共享内存。
.flatten() 总会返回一个拷贝（Copy），虽然慢一点，但更安全，因为修改它不会影响原数组。

array.ravel(order='C')

参数	说明
`order`	（可选）指定读取顺序，`'C'` 为行优先，`'F'` 为列优先。

array.flatten(order='C')

参数	说明
`order`	（可选）行为与 `ravel` 相同，但始终返回副本。

# ravel() 返回视图
raveled_view = reshaped.ravel()
raveled_view[0] = 100
print(f"\nRaveled (view): {raveled_view}")
print(f"Original reshaped array was changed: \n{reshaped}")

raveled_fortran = reshaped.ravel(order='F')
print(f"Raveled with column-major order: {raveled_fortran}")

# flatten() 返回拷贝
flattened_copy = reshaped.flatten()
flattened_copy[1] = 200
print(f"\nFlattened (copy): {flattened_copy}")
print(f"Original reshaped array was NOT changed: \n{reshaped}")

flattened_fortran = reshaped.flatten(order='F')
print(f"Flattened with column-major order: {flattened_fortran}")

转置 (.T): 交换数组的行和列，返回一个视图。这在线性代数中是基础且频繁的操作。

# reshaped 是一个 3x4 的数组
print(f"\nOriginal reshaped array (3x4):\n{reshaped}")

# 获取转置
transposed = reshaped.T
print(f"\nTransposed array (4x3):\n{transposed}")

添加新维度 (np.newaxis): 有时我们需要给数组增加一个“空”维度，例如，将一个一维向量转换为二维的行向量或列向量，以便它能参与矩阵运算或广播。np.newaxis (它其实就是 None 的一个别名) 可以轻松实现这一点。

vec = np.arange(4)
print(f"\nOriginal vector (shape {vec.shape}): {vec}")

# 在列的位置上增加一个维度，将其变为列向量
col_vec = vec[:, np.newaxis]
print(f"\nColumn vector (shape {col_vec.shape}):\n{col_vec}")

# 在行的位置上增加一个维度，将其变为行向量
row_vec = vec[np.newaxis, :]
print(f"\nRow vector (shape {row_vec.shape}):\n{row_vec}")

2. 数组拼接

在数据处理中，我们常常需要将来自不同来源的、分散的数组合并成一个大数组。

np.vstack() 或 np.concatenate(axis=0): 垂直拼接（沿着 axis=0），增加行数。

np.vstack(arrays) / np.concatenate(arrays, axis=0)

参数	说明
`arrays`	（必选）一个数组序列，所有数组在除目标轴外的形状必须一致。
`axis`	（可选）对 `np.concatenate` 有效，设置拼接方向，垂直拼接时为 0。

np.hstack() 或 np.concatenate(axis=1): 水平拼接（沿着 axis=1），增加列数。

np.hstack(arrays) / np.concatenate(arrays, axis=1)

参数	说明
`arrays`	（必选）一个数组序列，水平方向拼接时行数必须一致。
`axis`	（可选）对 `np.concatenate` 有效，水平拼接时为 1。

A = np.ones((2, 3))
B = np.zeros((2, 3))

# 垂直拼接
v_stack = np.vstack((A, B))
concat_axis0 = np.concatenate((A, B), axis=0)
print("Vertical Stack (vstack):")
print(v_stack)
print("Using concatenate axis=0 yields same result:")
print(concat_axis0)

# 水平拼接
h_stack = np.hstack((A, B))
concat_axis1 = np.concatenate((A, B), axis=1)
print("\nHorizontal Stack (hstack):")
print(h_stack)
print("Using concatenate axis=1 yields same result:")
print(concat_axis1)

3. 数组排序

排序是数据分析中最基本的操作之一。NumPy 提供了简单高效的排序功能。

np.sort(): 这是一个函数，它返回一个排序后的新数组（拷贝），而不改变原数组。

np.sort(a, axis=-1)

参数	说明
`a`	（必选）要排序的数组。
`axis`	（可选）指定排序的轴，默认对最后一个轴排序，设为 `None` 时会展平成一维。

data = rng.integers(0, 100, size=10)
print(f"\nUnsorted data: {data}")

# 使用 np.sort()
sorted_copy = np.sort(data)
print(f"Sorted copy:   {sorted_copy}")
print(f"Original data is unchanged: {data}")

.sort(): 这是一个数组自身的方法，它会就地排序（in-place），直接修改原数组，不返回任何值。

# 使用 .sort() 方法
data.sort()
print(f"Data sorted in-place: {data}")

# 在二维数组上比较 axis 参数
matrix = rng.integers(0, 50, size=(2, 4))
print(f"\nOriginal matrix:\n{matrix}")

sorted_rows = np.sort(matrix, axis=1)
print(f"Sorted along rows (axis=1):\n{sorted_rows}")

matrix_column_sort = matrix.copy()
matrix_column_sort.sort(axis=0)
print(f"Sorted in-place along columns (axis=0):\n{matrix_column_sort}")

4. 广播 (Broadcasting)

广播是 NumPy 最强大的功能之一，它让我们可以在不同形状的数组之间执行算术运算，而无需显式地创建循环或复制数据。当两个数组的维度不完全匹配时，NumPy 会自动“延展”较小的数组，使其形状与较大数组兼容。

你可以想象一个 3x3 的矩阵，你想给它的每一行都加上一个 1x3 的向量。广播会自动将这个向量“延展”三遍，然后执行逐元素的加法，非常高效。

np.broadcast_to(): 将数组广播到目标形状，生成一个视图（或在必要时创建拷贝），以便与更大维度的数组进行运算。

np.broadcast_to(array, shape, subok=False)

参数	说明
`array`	（必选）需要被广播的原始数组。
`shape`	（必选）目标形状，需与广播规则兼容。
`subok`	（可选）是否保留子类类型，默认为 `False`。

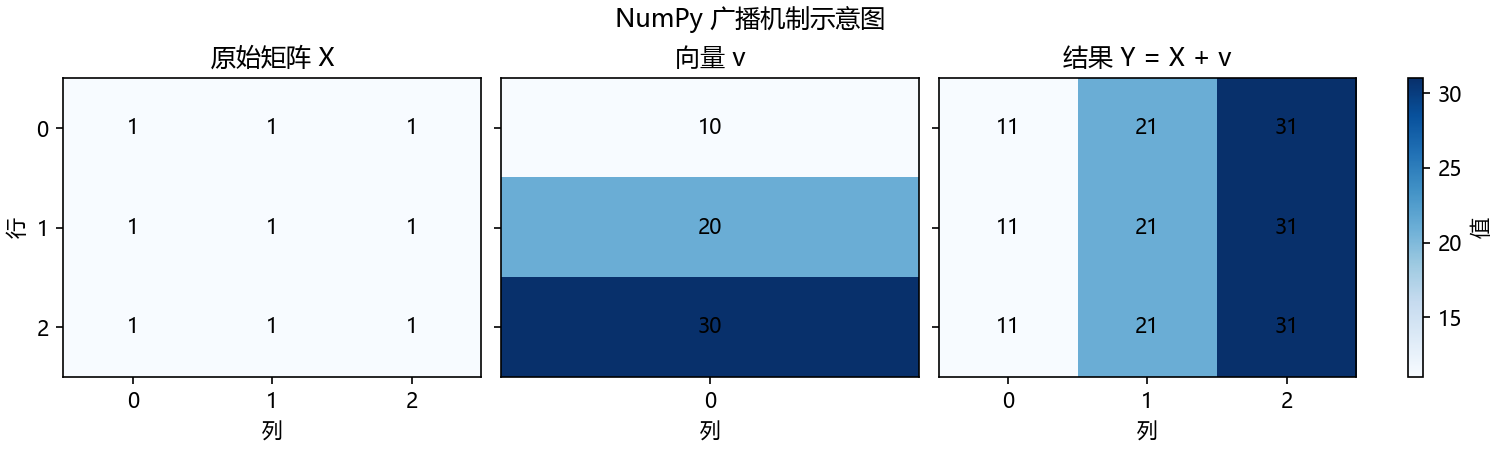
X = np.ones((3, 3))      # Shape: (3, 3)
v = np.array([10, 20, 30])  # Shape: (3,)

# 使用 np.broadcast_to 将向量显式广播为矩阵视图
v_broadcasted = np.broadcast_to(v, X.shape)

# 广播规则检查维度，从后往前：
# 1. v 的维度1 (size 3) 与 X 的维度2 (size 3) 匹配。
# 2. v 没有维度2，但 X 有维度1 (size 3)。broadcast_to 会在前面“新增”一个维度并“复制”自己来匹配。
# 最终，v_broadcasted 表现得像一个 (3, 3) 的数组 [[10, 20, 30], [10, 20, 30], [10, 20, 30]]
Y = X + v_broadcasted
print(f"\nBroadcasting a vector to each row:\n{Y}")

5. 矩阵乘法

在 NumPy 中，* 操作符执行的是逐元素乘法，而不是标准的矩阵乘法。为了执行矩阵乘法，你需要使用 @ 操作符（推荐）或 np.matmul() 函数。这对于任何涉及线性代数的计算都至关重要。

np.matmul(): 计算两个数组的矩阵乘法，支持二维及更高维数组的批量乘法。

np.matmul(x1, x2, out=None)

参数	说明
`x1`	（必选）左侧输入数组，其最后一维与 `x2` 的倒数第二维匹配。
`x2`	（必选）右侧输入数组，其倒数第二维与 `x1` 的最后一维匹配。
`out`	（可选）用于存放结果的目标数组，需具备正确形状。

mat_A = np.arange(6).reshape(2, 3)
mat_B = np.arange(6).reshape(3, 2)

print(f"Matrix A (2x3):\n{mat_A}")
print(f"\nMatrix B (3x2):\n{mat_B}")

# 使用 np.matmul 进行矩阵乘法（与 @ 等价）
mat_product = np.matmul(mat_A, mat_B)
print(f"\nMatrix Product A @ B (2x2):\n{mat_product}")

四、通用函数 (ufunc) 与统计

为了发挥 NumPy 的速度优势，我们应该始终优先使用它提供的函数（称为 ufuncs, Universal Functions）来对整个数组进行数学运算和统计计算。

1. 向量化运算 (ufuncs)

所谓的“向量化”，就是避免写 Python for 循环，直接对整个数组调用函数。这不仅代码更短，速度也快得多。

np.add(): 对两个数组（或数组与标量）执行逐元素加法，是 + 运算符背后的 ufunc。

np.add(x1, x2, out=None, where=True)

参数	说明
`x1`	（必选）第一个输入数组或标量。
`x2`	（必选）第二个输入数组或标量，形状需与 `x1` 广播兼容。
`out`	（可选）用于存放结果的数组，形状需与输出一致。
`where`	（可选）仅在条件为 `True` 的位置执行运算。

np.sqrt(): 计算数组每个元素的平方根。

np.sqrt(x, /, out=None, where=True)

参数	说明
`x`	（必选）输入数组或标量。
`out`	（可选）用于存放结果的数组。
`where`	（可选）用于屏蔽输出的布尔条件。

提示

在 Python 中，函数定义里出现 / 表示在它之前的参数只能通过位置传递，不能用关键字传递。所以在 np.sqrt(x, /, out=None, where=True) 中，你可以忽略掉 / , 理解为 np.sqrt(x, out=None, where=True) 即可。

np.sin(): 计算数组每个元素的正弦值，输入以弧度为单位。

np.sin(x, /, out=None, where=True)

参数	说明
`x`	（必选）输入数组或标量。
`out`	（可选）用于存放结果的数组。
`where`	（可选）用于屏蔽输出的布尔条件。

data = np.arange(1, 6)
print(f"Original data: {data}")

# 逐元素加法
data_plus_10 = np.add(data, 10)
print(f"Add 10: {data_plus_10}")

# 逐元素开方
sqrt_data = np.sqrt(data)
print(f"Square root: {sqrt_data}")

# 逐元素计算三角函数
sin_data = np.sin(data)
print(f"Sine: {sin_data}")

2. 描述性统计与 `axis` 参数

快速计算数组的总和、均值、最大/最小值等是数据分析的日常。axis 参数是这里的核心，它让我们能指定是按列、按行还是对整个数组进行计算。

你可以把 axis 理解为“将被折叠/聚合掉的那个维度”。在一个二维数组中：

axis=0: 沿着行的方向进行操作，折叠所有行，最终对每一列进行计算。
axis=1: 沿着列的方向进行操作，折叠所有列，最终对每一行进行计算。

np.sum(): 计算数组元素之和，可指定沿哪一个轴聚合。

np.sum(a, axis=None, dtype=None, keepdims=False)

参数	说明
`a`	（必选）输入数组或类数组对象。
`axis`	（可选）指定聚合轴，`None` 表示对全部元素求和。
`dtype`	（可选）指定返回结果的数据类型。
`keepdims`	（可选）是否保留被聚合轴的维度。

np.mean(): 计算数组元素的均值，同样支持按轴聚合。

np.mean(a, axis=None, dtype=None, keepdims=False)

参数	说明
`a`	（必选）输入数组或类数组对象。
`axis`	（可选）指定聚合轴。
`dtype`	（可选）指定返回结果的数据类型。
`keepdims`	（可选）是否保留被聚合轴的维度。

data = rng.integers(0, 10, size=(3, 5))
print(f"\nData:\n{data}")

# 对整个数组计算
total_sum = np.sum(data)
print(f"Overall sum (axis=None): {total_sum}")

# 沿着 axis=0 计算每一列的总和
col_sums = np.sum(data, axis=0)
print(f"Sum of each column (axis=0): {col_sums}")

# 沿着 axis=1 计算每一行的均值
row_means = np.mean(data, axis=1)
print(f"Mean of each row (axis=1): {row_means}")

3. 条件化操作 `np.where()`

在数据处理中，我们经常需要根据某个条件来对数组中的元素进行赋值，例如：“如果元素大于0，则设为1，否则设为-1”。如果使用循环来做，效率会很低。np.where() 就是为此而生的强大工具，它等价于一个向量化的 if-else 语句，让这类操作变得非常高效。

语法: np.where(condition, x, y)

condition: 一个布尔数组。
x: 当 condition 中对应位置为 True 时，从 x 中取值。
y: 当 condition 中对应位置为 False 时，从 y 中取值。

np.where(condition, x=None, y=None)

参数	说明
`condition`	（必选）布尔数组或可广播为布尔数组的条件表达式。
`x`	（可选）条件为 `True` 时选取的值或数组；缺省时返回满足条件的索引。
`y`	（可选）条件为 `False` 时选取的值或数组；与 `x` 需可广播兼容。

# 创建一个随机的正态分布数组
cond_data = rng.standard_normal((3, 4))
print(f"\nOriginal conditional data:\n{cond_data}")

# 使用 np.where 将所有正数替换为 1，所有负数替换为 -1
where_result = np.where(cond_data > 0, 1, -1)
print(f"\nResult after np.where(cond_data > 0, 1, -1):\n{where_result}")

4. 唯一值与集合操作 (Unique Values & Set Logic)

除了找出不重复的元素，我们有时还需要进行集合类的比较，比如判断一个数组中的元素是否存在于另一个数组中。

np.unique(): 找出数组中的唯一值并返回排序后的结果。

np.unique(ar, return_index=False, return_inverse=False, return_counts=False, axis=None)

参数	说明
`ar`	（必选）输入数组或类数组对象。
`return_index`	（可选）是否返回去重值在原数组中的索引。
`return_inverse`	（可选）是否返回原数组对应唯一值的索引。
`return_counts`	（可选）是否返回每个唯一值的出现次数。
`axis`	（可选）沿指定轴去重，默认对展平后的数组操作。

data_with_dupes = np.array([1, 2, 1, 3, 5, 2, 1, 1, 5])
print(f"\nOriginal data with duplicates: {data_with_dupes}")

unique_values = np.unique(data_with_dupes)
print(f"Unique values: {unique_values}") # [1 2 3 5]

np.in1d(): 判断一个数组（第一个参数）中的元素是否存在于另一个数组（第二个参数）中，返回一个布尔数组。这在数据筛选时非常有用。

np.in1d(ar1, ar2, assume_unique=False, invert=False)

参数	说明
`ar1`	（必选）需要检查的数组。
`ar2`	（必选）参照数组，用于判断成员关系。
`assume_unique`	（可选）如为 `True`，假定输入已唯一，可加速计算。
`invert`	（可选）是否返回非成员关系的结果。

# 检查 data_with_dupes 中的每个元素是否在 [2, 3, 4] 中出现过
values_to_check = [2, 3, 4]
membership_mask = np.in1d(data_with_dupes, values_to_check)
print(f"\nIs element in {values_to_check}? {membership_mask}")

# 结合布尔索引，我们可以选出所有在 `values_to_check` 中的元素
elements_found = data_with_dupes[membership_mask]
print(f"Elements found in {values_to_check}: {elements_found}")

五、保存与加载数组

计算完成后，我们通常需要将结果持久化到磁盘，以便将来可以重新加载使用，而无需再次计算。NumPy 提供了简单高效的二进制格式 .npy 和 .npz。

np.save(): 将单个数组保存到 .npy 文件中。

np.save(file, arr, allow_pickle=False, fix_imports=True)

参数	说明
`file`	（必选）目标文件路径或类文件对象。
`arr`	（必选）要保存的数组。
`allow_pickle`	（可选）是否允许保存 Python 对象（基于 pickle）。
`fix_imports`	（可选）在 Python 2/3 间转换时修复导入问题。

# 保存之前的矩阵 M 到 .npy 文件 (NumPy 原生二进制格式)
np.save('my_array.npy', M)
print("\nArray M saved to my_array.npy")

np.load(): 从 .npy 文件加载数组。

np.load(file, mmap_mode=None, allow_pickle=False, fix_imports=True, encoding='ASCII')

参数	说明
`file`	（必选）包含数组数据的文件路径或类文件对象。
`mmap_mode`	（可选）使用内存映射模式加载大文件，如 `'r'`、`'r+'`。
`allow_pickle`	（可选）是否允许加载被 pickle 序列化的对象。
`fix_imports`	（可选）在 Python 2/3 间转换时修复导入问题。
`encoding`	（可选）读取 pickled 对象的编码方式。

# 从 .npy 文件加载数组
loaded_M = np.load('my_array.npy')
print("Array loaded from my_array.npy:")
print(loaded_M)

np.savez(): 将多个数组保存到一个未压缩的 .npz 文件中（使用 ZIP 容器按名称存储多个数组）。

np.savez(file, *args, **kwds)

参数	说明
`file`	（必选）输出文件路径或类文件对象。
`*args`	（可选）未命名的数组序列，将按顺序命名为 `arr_0`, `arr_1`, …。
`**kwds`	（可选）以关键字形式指定的数组，会使用提供的名称保存。

# 将多个数组保存到 .npz 文件
np.savez('my_arrays.npz', array_x=X, array_y=Y)
print("\nArrays X and Y saved to my_arrays.npz")

# 加载 .npz 文件
loaded_data = np.load('my_arrays.npz')
print("Loaded array_x from .npz file:")
print(loaded_data['array_x'])

实践小结: 你已经掌握了 NumPy 最核心的数组创建、索引、操作和计算方法。请务-必花时间理解视图与拷贝的区别、广播的原理以及 axis 参数的用法，这些是高效使用 NumPy 和 Pandas 的关键。下一章，我们将学习更专注于表格数据处理的 Pandas 库。

2. NumPy 快速上手：数组与向量化计算

2. NumPy 快速上手：数组与向量化计算

NumPy: Python 数据科学的基石

准备工作

一、创建 `ndarray`：构建你的数据块

1. 从 Python 列表创建

2. 使用内置函数创建占位符数组

3. 创建序列数组

4. 创建随机数组

5. 数组的基本属性

二、索引与切片：精准获取数据

1. 基础索引与切片

2. 布尔索引

3. 花式索引 (Fancy Indexing)

三、核心数组操作

1. 形状变换

2. 数组拼接

3. 数组排序

4. 广播 (Broadcasting)

5. 矩阵乘法

四、通用函数 (ufunc) 与统计

1. 向量化运算 (ufuncs)

2. 描述性统计与 `axis` 参数

3. 条件化操作 `np.where()`

4. 唯一值与集合操作 (Unique Values & Set Logic)

五、保存与加载数组

results matching ""

No results matching ""

2. NumPy 快速上手：数组与向量化计算

NumPy: Python 数据科学的基石

准备工作

一、创建 ndarray：构建你的数据块

1. 从 Python 列表创建

2. 使用内置函数创建占位符数组

3. 创建序列数组

4. 创建随机数组

5. 数组的基本属性

二、索引与切片：精准获取数据

1. 基础索引与切片

2. 布尔索引

3. 花式索引 (Fancy Indexing)

三、核心数组操作

1. 形状变换

2. 数组拼接

3. 数组排序

4. 广播 (Broadcasting)

5. 矩阵乘法

四、通用函数 (ufunc) 与统计

1. 向量化运算 (ufuncs)

2. 描述性统计与 axis 参数

3. 条件化操作 np.where()

4. 唯一值与集合操作 (Unique Values & Set Logic)

五、保存与加载数组

results matching ""

No results matching ""

一、创建 `ndarray`：构建你的数据块

2. 描述性统计与 `axis` 参数

3. 条件化操作 `np.where()`